《随机过程》是一门利用数学方法解决实际动态随机问题的应用数学学科,但是现有《随机过程》学科的研究方法却违背随机现象“个别不确定”的客观事实,假定随机现象个别结果也具有确定性的规律,在数学抽象过程中不仅违背了其它学科的函数、概率、正态分布等基本概念,而且也违背了《随机过程》学科的随机过程定义,混淆了样本函数与随机变量的区别,甚至在定义、推理或证明过程中出现了违反同一律和矛盾律的逻辑错误,建立的理论不仅与函数、概率、正态分布和随机过程等数学基本概念冲突,而且理论与经验事实不符,逻辑上不能自洽。因此在《随机过程》教学过程中,越是基本概念清晰的学生就越是无法理解《随机过程》教科书的定义及结论,导致《随机过程》成为各高校挂科率最高的课程之一,广为流传的“随机过程随机过”段子并不是调侃,而是《随机过程》学科期末考试结果的真实写照。
知乎问答显示,北大数院的《应用随机过程》位于北京大学的挂科率榜首,清华大学电子系的《随机过程》挂科率也高达30%。若想顺利通过《随机过程》考试,必须要痛苦地放弃在其它课程中已经建立起来的数学基本概念及理论,接受《随机过程》违背基本常识的错误方法及错误理论,因此《随机过程》是一门让所有学生在学习时感到恐惧、在考试时濒临崩溃的反常课程。
一、研究方法违背随机现象“个别不确定”的客观事实
随机现象是指在一次试验中其结果呈现出不确定性 ,但是在大量重复试验中其结果又具有确定性统计规律的现象。
例如在抛硬币试验中,虽然每次抛出硬币后的结果完全随机、毫无规律、无法预测,但是随着抛硬币次数的逐渐增大,所有试验结果就会呈现出50%正面向上和50%反面向上的确定性统计分布规律。
假设第i次抛出硬币后的结果为x(i),若硬币正面向上,令x(i)=1;若硬币反面向上,令x(i)=-1,则连续n次抛硬币试验观察结果就构成一个按时间顺序形成的随机时间序列
x(1),x(2),…,x(i),…,x(n)
假设上述随机时间序列中有nH个序列值等于1,nT个序列值等于-1,则硬币正面向上事件和反面向上事件出现的概率分别为
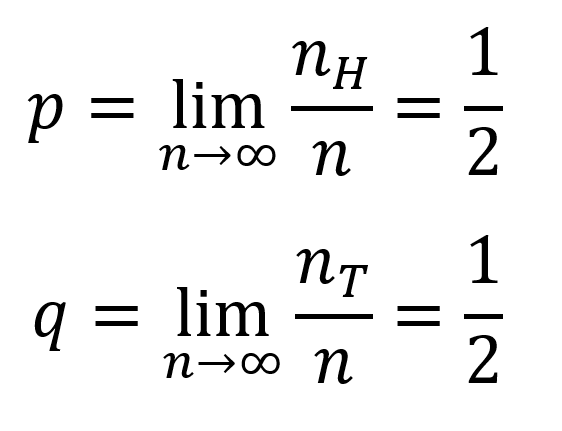
#FormatImgID_1#
若每一次硬币抛出后,正、反面出现的概率均为1/2,则意味着每一次硬币被抛出后,硬币必然会一分为二,出现半个硬币正面向上和半个硬币反面向上的荒谬结果。
二、数学抽象违背函数基本概念
函数定义: 在一个变化过程中,假设有两个变量x、y,如果对于任意一个x都有唯一确定的一个y和它对应,则称变量y为变量x的函数,记作
y=f(x)
其中变量x称为自变量,变量y称为因变量或函数。
函数f(x)通常有三种表示方法:解析法、列表法和图像法。
观察质点位移x(t)随时间t的变化过程(图1),无论质点做确定性运动还是随机性运动,在每一个确定的时刻t,都有唯一一个确定的质点位置x(t)与时间t “一一对应”,因此,质点位移x(t)与时间t之间的数量关系为函数关系。
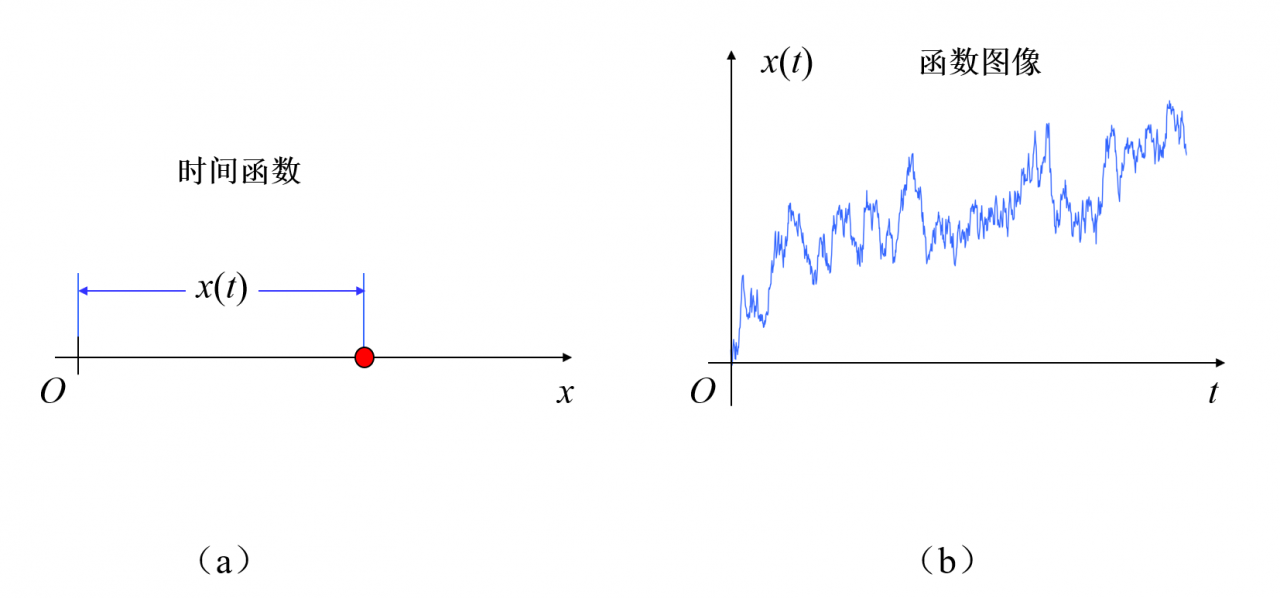
但是,《随机过程》在研究随机运动的质点位移与时间之间的数量关系时,竟将质点位移与时间之间的数量关系抽象为随机变量x(t),而随机变量x(t)是定义在样本空间Ω上的函数,其自变量为样本点ω(表1),随机变量x(t)在t时刻的取值有多个或无穷多个 。
表1 时间函数与随机变量的区别

概率定义: 在相同条件下重复进行n次试验,其中事件A发生的次数为nA,如果随着试验次数n的增多,事件A发生的频率nA/n会稳定在某个常数p附近 ,那么这个常数p就叫做事件A的概率。
对于抛硬币试验,当n=1时,频率不是0就是1,根本不存在稳定的频率值。但是,《随机过程》仍然定义每一次抛硬币结果出现正面向上的概率p=1/2,歪曲了概率定义的内涵及外延。
四、违背正态分布基本概念
自从1809年德国数学家高斯(Gauss)发现测量误差服从正态分布(图2)后,人们发现正态分布在自然界和人类社会实践活动中极为常见。
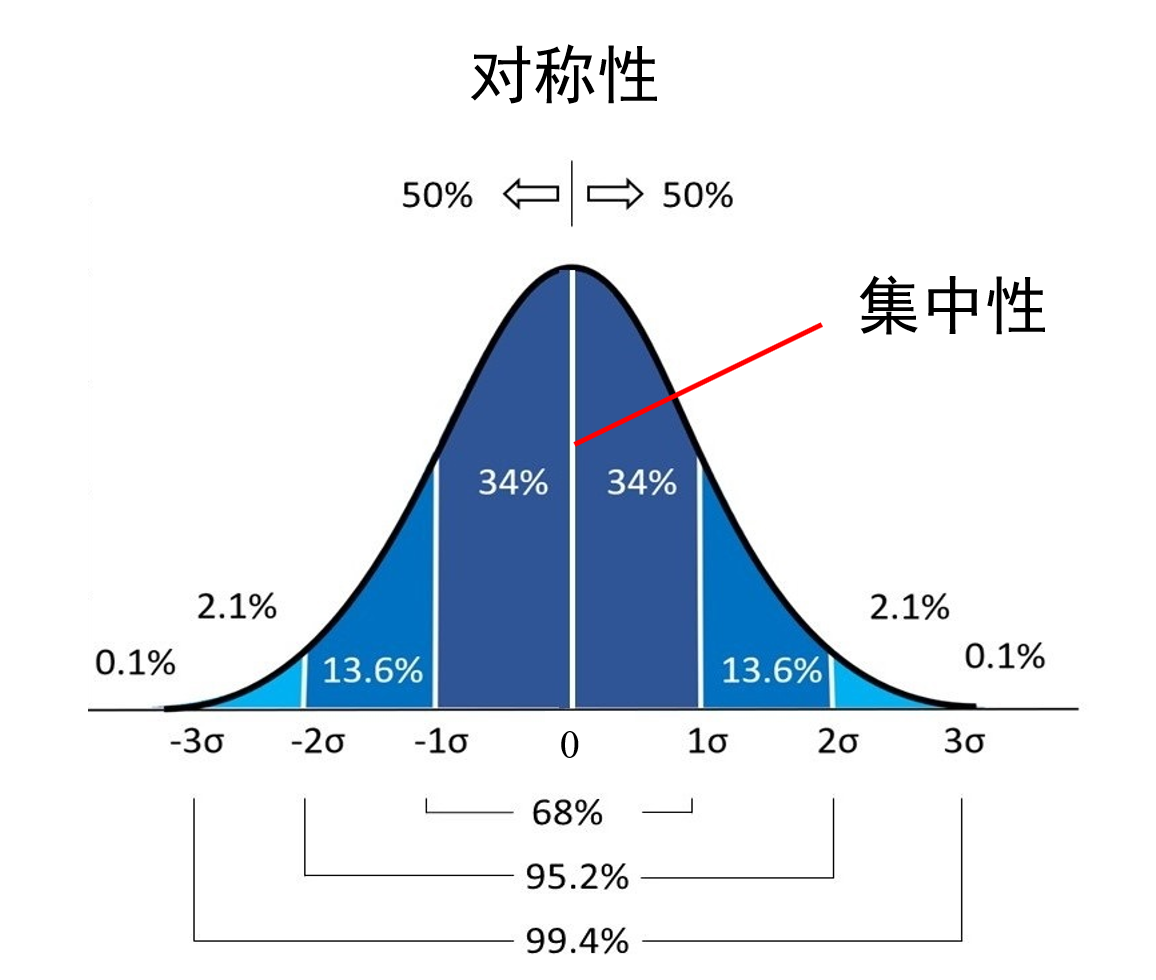
正态分布具有如下两个重要的特征:
(1)对称性 。绝对值相等的正、负样本数据出现的次数大致相等。
(2)集中性 。绝对值小的样本数据比绝对值大的样本数据出现的次数多。
图3是服从正态分布的高斯白噪声函数图像,显然具有正态分布的对称性 和集中性 。
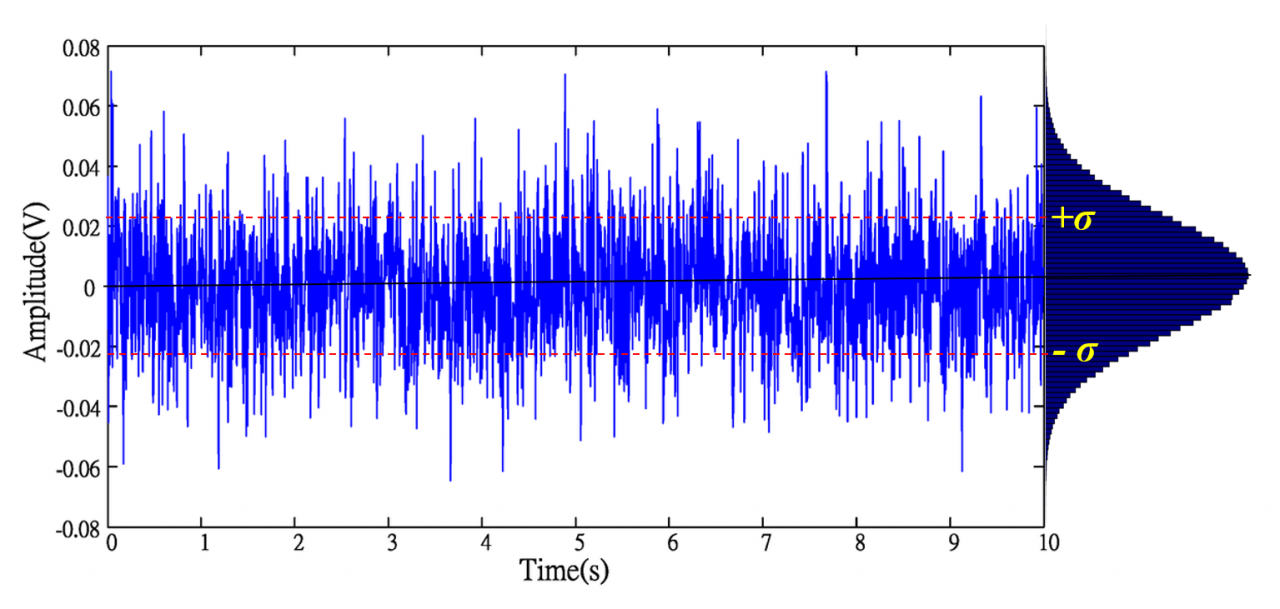
观察图1(b)所示的布朗粒子位移曲线,根本不具有正态分布的对称性 和集中性 ,但是,维纳过程定义却假定图1(b)所示的布朗粒子位移曲线服从正态分布。
五、违背随机过程定义
随机过程 X(t)是定义在Ω×T上的二元函数X(ω,t)。对于固定的时间t,X(ω,t)是样本点ω的函数,称为随机变量,记为X(t);对于固定的样本点ω,X(ω,t)是时间t的函数,称为样本函数或样本轨道,记为x(t)。
一个样本函数x(t)对应着随机试验中的一次“测量结果”,即人们实际观察到的随机现象随时间演变过程,因此x(t)也被称为随机过程的一个“实现”,
图4为随机过程X(ω,t)、随机变量X(t)和样本函数x(t)三者之间的关系示意图。
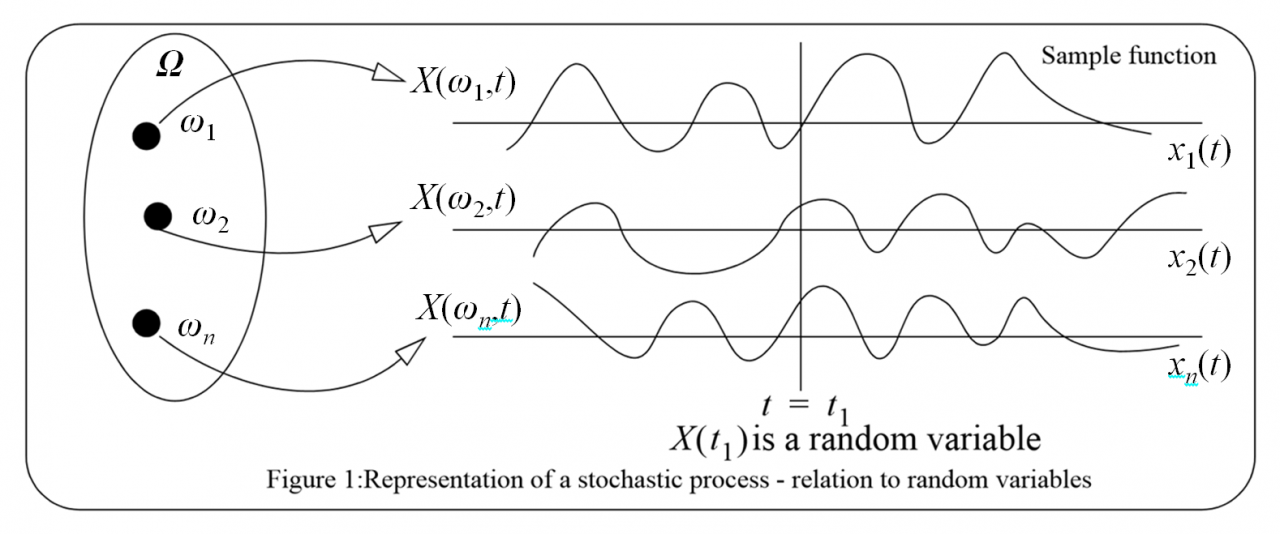
图4中的三条样本函数曲线x1(t),x2(t)和x3(t)可分别看成是三个随机运动质点的位移曲线,因此,随机过程X(ω,t)即可成是所有样本轨道x(t)的集合,也可看成是所有随机变量X(t)的集合。
从图4可以看出,随机变量X(t)和样本函数x(t)具有完全不同的物理意义。随机变量X(t)用来描述大量质点的空间位置分布规律,样本函数x(t)则用来描述一个质点的时间运动规律 。
随机变量X(t)和样本轨道x(t)是两个具有完全不同内涵与外延的单值函数,但是,《随机过程》在研究随机游走和布朗运动样本轨道的性质时,却将样本轨道x(t)当作随机变量X(t) ,因而出现了一系列理论与事实不符和逻辑上不能自洽的反常问题。
六、结论与物理学理论和实验结果不符
图5为物理学布朗运动位移和瞬时速度的实验曲线,其中图5(a)和(b)分别为一个布朗粒子的位移曲线和瞬时速度曲线,图5(c)和(d)分别为大量布朗粒子的位移曲线和瞬时速度曲线。
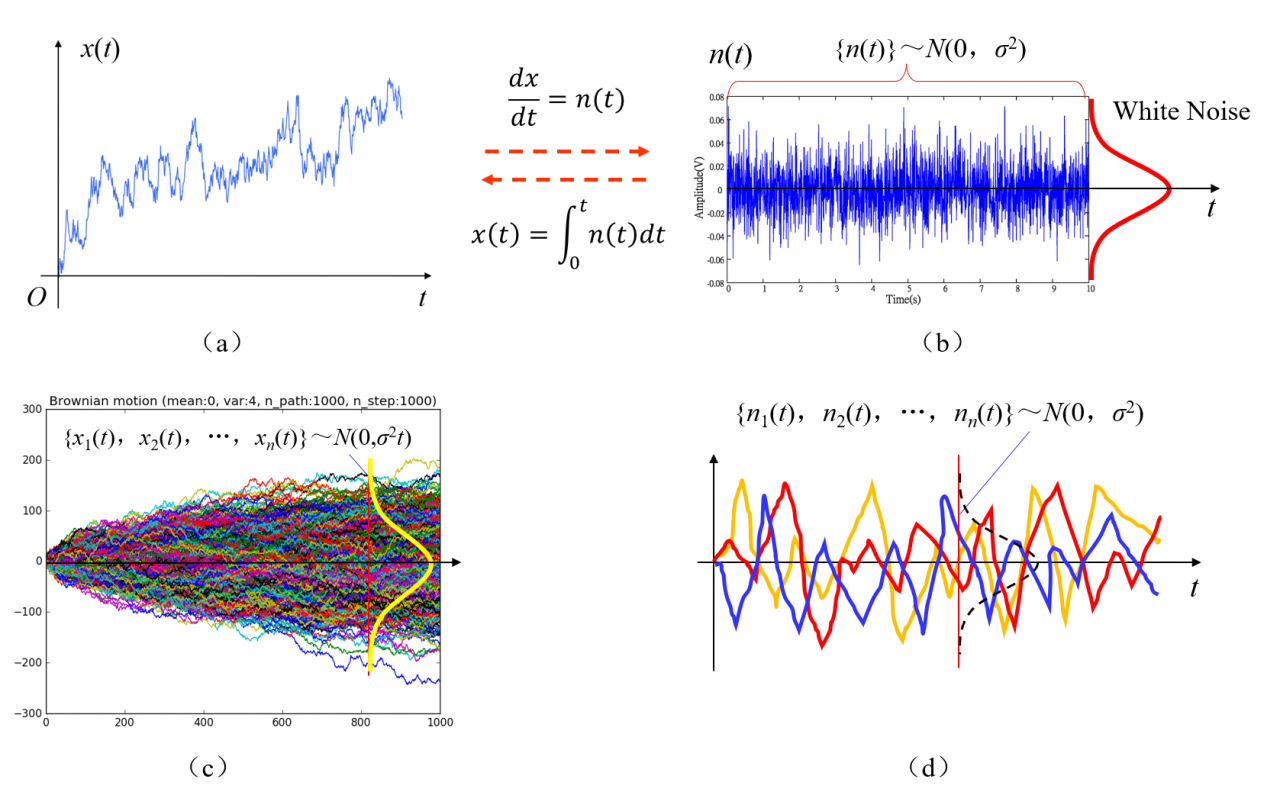
物理学布朗运动理论和实验结果表明:
(1)一个布朗粒子的瞬时速度在不同时刻的取值服从(0,σ2)正态分布;
(2)所有布朗粒子的瞬时速度在同一时刻的取值服从(0,σ2)正态分布;
(3)所有布朗粒子的位移在同一时刻的取值服从(0,σ2t)正态分布。
在图5中,只有图5(a)所示的一个布朗粒子的位移曲线不服从正态分布 。
《随机过程》教科书根据维纳过程定义,推导出了一个布朗粒子的位移服从(0,σ2t)正态分布和瞬时速度无穷大(处处不可导)的结论,与物理学布朗运动理论和实验结果完全不符。
事实上,《随机过程》学科认错了对象,弄错了事实,竟然张冠李戴,将刻画大量布朗粒子集体行为的正态分布用来描述一个布朗粒子的个体行为 ,这就如同用描述大量分子热运动集体行为的温度来度量一个分子的动能一样荒谬。
七、违反逻辑推理同一律
同一律的内容是:在同一推导、演算和分析过程中,所使用的概念必须要与其自身始终保持同一 。同一律要求逻辑推理过程必须具有确定性,也就是说,无论一个概念被使用或重复多少次,这个概念的内涵和外延必须是确定的。
如果在同一定义、推理或证明过程中,把两个内涵与外延完全不同的概念混为一个概念,不能保持概念内涵和外延的确定和同一,就会违反同一律,犯“混淆概念”或“偷换概念”的逻辑错误,导致推导出的结论自相矛盾,逻辑上不能自洽。
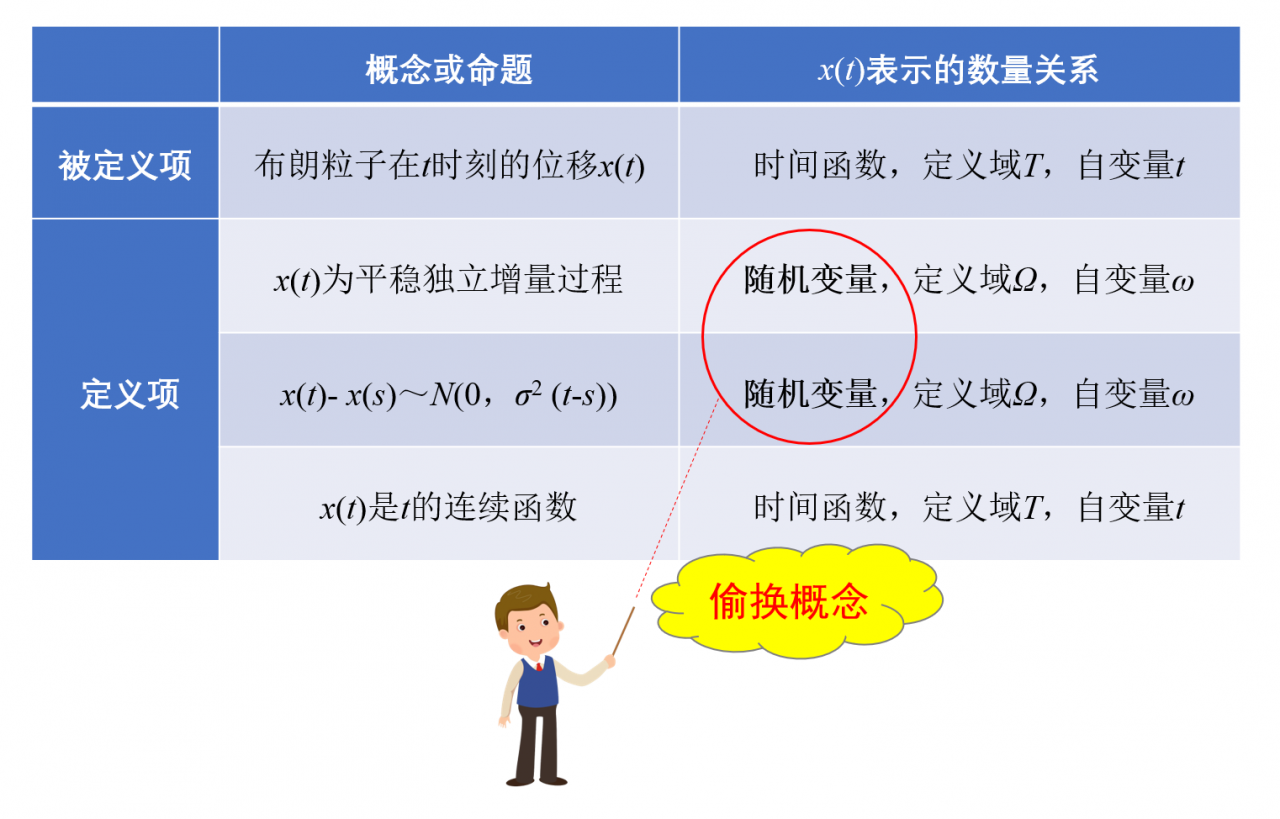
表2为维纳过程定义分析,虽然定义项(3)保持了被定义项布朗粒子位移x(t)时间函数概念的确定和同一,但是定义项(1)和定义项(2)没有保持被定义项x(t)时间函数概念的确定和同一,违背了逻辑推理的同一律要求 ,从而产生了“混淆概念”或“偷换概念”的逻辑错误。
表2 维纳过程定义逻辑错误分析
矛盾律的基本内容是:在同一思维过程中,两个不同的数学概念不能反映同一对象 。如果用两个不同的数学概念描述同一对象,就会出现违反矛盾律的逻辑错误,必然会导致逻辑矛盾或逻辑悖论的产生。
从表2可以看出,维纳过程的定义项使用随机变量和时间函数这两个内涵与外延完全不同的数学概念来描述同一对象,出现了违背矛盾律的逻辑错误。
八、结论
现有《随机过程》学科的研究方法违背随机现象“个别不确定”的客观事实,在数学抽象过程中不仅违背函数、概率、正态分布等数学基本概念,而且更为搞笑的是,竟然会违背自身的随机过程定义,混淆样本函数与随机变量的区别,甚至在定义、推理或证明过程中出现了违反同一律和矛盾律的逻辑错误,建立的理论不仅与函数、概率、正态分布和随机过程等数学基本概念冲突,而且与经验事实严重不符,逻辑上不能自洽,是一门货真价实的“伪科学”。
 社科在线
社科在线




