本文介绍近代数学的若干个数学学派。篇幅较短,只是希望读者能有一个大致的认识。就好比逛一下博物馆,先做走马观花状,待于一处兴致颇浓,再做深入研究,也未尝不可。其实,学习各学派发展的兴衰史,有助于我们了解数学自身的发展规律,包括数学在一个地区或国家发展兴衰的启示。
来源 | 数学与人工智能
1
格丁根学派
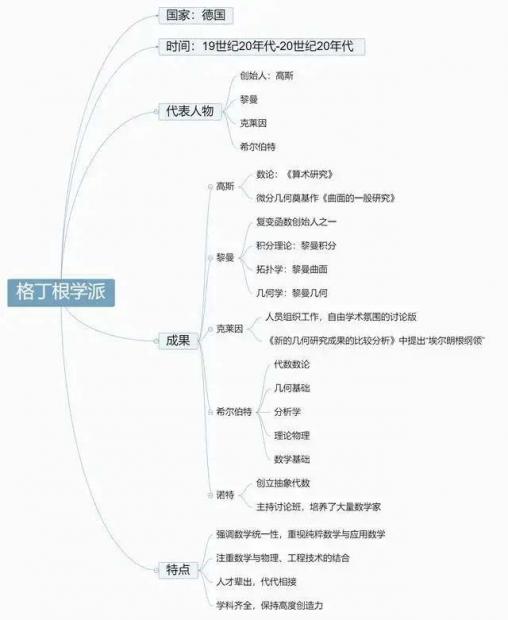
德国19世纪20年代到20世纪20年代,由高斯(Gauss)创始,黎曼(Georg Friedrich Bernhard Riemann)、克莱因(Felix Christian Klein)、希尔伯特(David Hilbert)等人发展致盛,在世界数学史中长期占主导地位的学派。格丁根学派强调数学的统一性,重视纯粹数学和应用数学,将数学理论与近代工程技术紧密结合。格丁根学派“兵多将广”且代代相接,学科齐全且长期保持着高度创造力。然而到20世纪30年代,纳粹执政后的疯狂民族主义导致该学派日渐衰退。
2
柏林学派
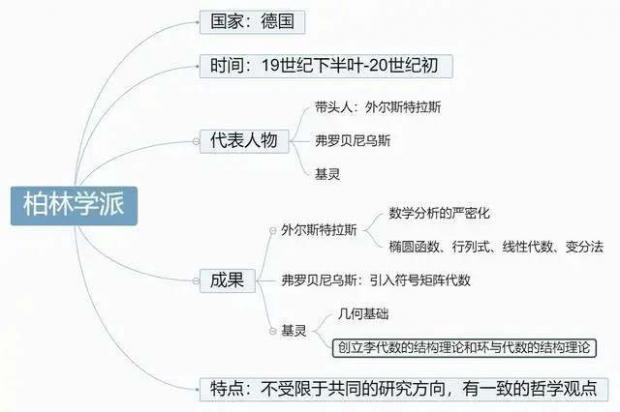
19世纪下半叶到20世纪初,德国柏林兴起的数学学派,其代表人物为外尔斯特拉斯(Karl Theodor Wilhelm Weierstrass)、弗罗贝尼乌斯(Frobenius Ferdinand Georg)、基灵(Wilhelm Killing)等人。柏林学派主要从事数学分析、符号代数和几何基础方面的研究。虽然柏林学派不受限于共同的研究方向,但有着一致的哲学观点,指导研究工作。
3
彼得堡学派
19世纪下半叶到20世纪初,在俄国圣彼得堡城兴起的学派,其代表人物为切比雪夫、马尔可夫、李亚普诺夫等人。彼得堡学派的主要特征是数学理论与实际应用紧密地结合,并在应用数学中做出了较大贡献。
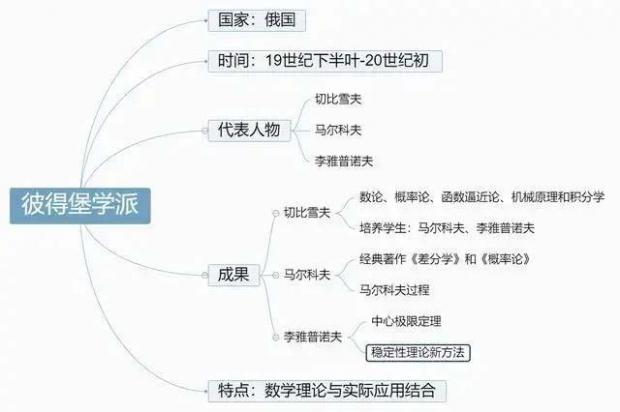
彼得堡学派是俄国(苏联)最早的数学学派,对苏联近代数学的发展产生过巨大影响。20世纪中,圣彼得堡(列宁格勒)又出现了坎托罗维奇等现代数学家,他们在继承和发展彼得堡学派的理论及传统方面做出了的贡献。
4
意大利代数几何学派
19世纪60年代兴起于意大利,由布廖斯基(Brioschi Francesco)、贝蒂(Enrico Betti)和克雷莫纳(Cremona,Antonio)“掌门”。该学派的工作在性质上属于古典代数几何,有着自己的风格和研究主题,代表了代数几何发展中的几何倾向,对意大利数学的全面发展有深远影响。
19世纪50年代开始,意大利数学家与欧洲数学有了广泛交流,使意大利摆脱了闭塞落后的局面。1863年,波伦亚大学的数学教授克雷莫纳给出平面曲线一般变换理论的阐述,此后又发展了被称为克雷莫纳变换:任意维射影空间的射影平面与有理平面的双有理变换理论。他的一系列工作成为意大利代数几何研究的起点,并激发了许多数学家的研究。
19世纪90年代后,意大利第二代代数几何学家成长起来,其中塞格雷(Segre Beniamino)于1894年扩展应用了曲线族中曲线在一条曲线上截得点的线性系的思想,启示后人发现许多新的双有理不变性质。19世纪末卡斯泰尔诺沃(Guido Castelnuovo)与恩里克斯(Federigo Enriques)开始合作,以线性系为中心概念进行研究。利用克雷莫纳变换奠定了代数曲面中曲线的线性系理论,并对曲面分类理论进行了深刻的研究。塞维里(Severi, Francesco)师从塞格雷,完善了代数曲面双有理不变量理论,并推广到任意维代数族上。他还建立了代数几何中的基础理论,为代数曲面上零维团链理论打下了基础。
5
法国函数论学派
19世纪末兴起于法国巴黎高等师范学校,以阿达马(Jacques Solomon Hadamard)、波莱尔(Borel Emile)、贝尔(Baire René-Louis)、勒贝格(Henri Léon Lebesgue)等人为代表。
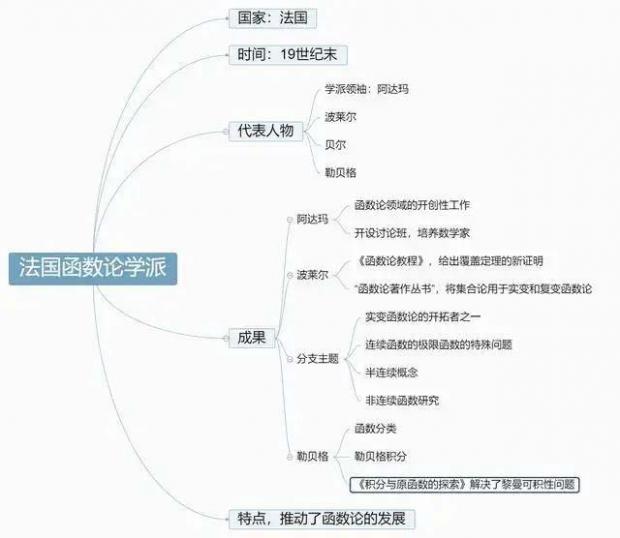
在20世纪初,法国函数论学派吸引了世界各地的学生,推动了世界函数论的发展。第一次世界大战使法国科学研究遭受重创,函数论学派的没落。法国数学在战后逐渐转向应用领域和公理化方法。
6
普林斯顿学派
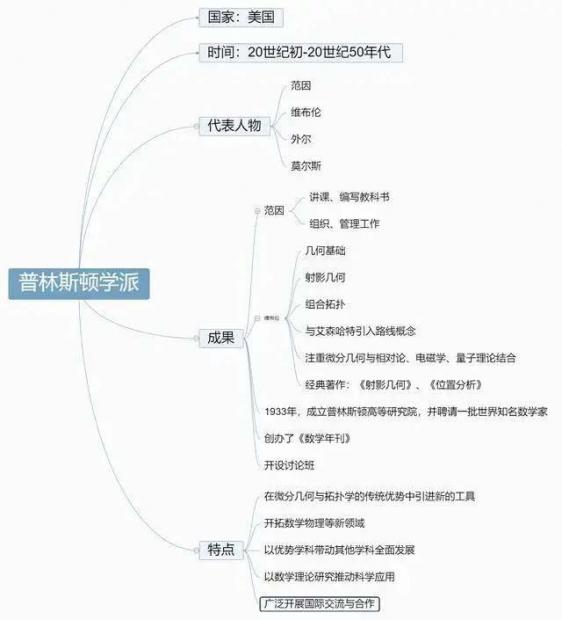
美国数学在19世纪后期才逐渐与欧洲数学接轨,而普林斯顿学派于20世纪初兴起于美国普林斯顿,并一直延续到20世纪50年代,以范因(H.B.Fine)、维布伦(Veblen Oswald)、外尔(Hermann Weyl)、莫尔斯(Morse HaroldMarston)等人为代表。普林斯顿学派既在微分几何与拓扑学的传统优势中引进新的工具,又开拓数学物理等新领域。以优势学科带动其他学科全面发展,以数学理论研究推动科学应用,并广泛开展国际交流与合作,是现代数学的发展的一种非常成功的模式。
7
莫斯科学派
20世纪初的苏联在莫斯科创立的学派,又细分为两个侧重不同的学派:由叶戈洛夫和卢津创始,柯尔莫哥洛夫等人发扬光大的函数论学派;以亚历山德罗夫、乌雷松、庞特里亚金等人为代表拓扑学派。
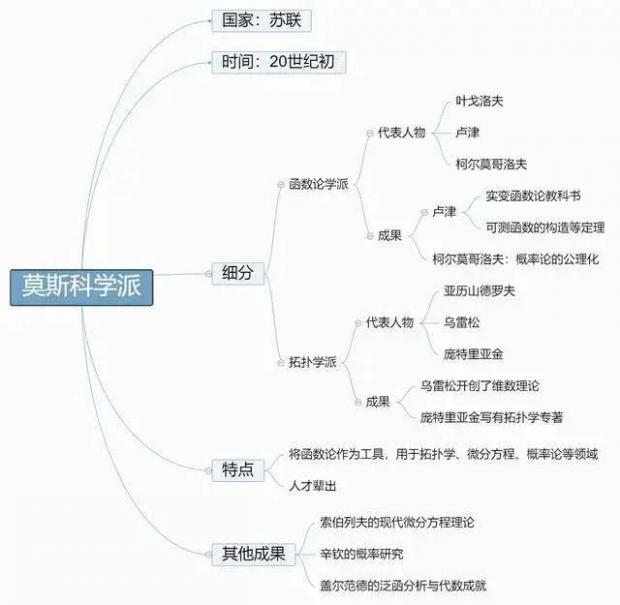
莫斯科学派将函数论作为工具,在拓扑学、微分方程、概率论等几个方面都获得长足发展,其中有较著名数学成果的还有索伯列夫的现代微分方程理论、辛钦的概率研究、盖尔范德的泛函分析与代数成就等。近年来莫斯科数学界仍然新人辈出,在他们中诺维科夫和马尔库利斯分别荣获1970年和1978年度菲尔兹奖。
8
剑桥分析学派
20世纪上半叶以英国剑桥大学为中心兴起,以哈代(Hardy Godfrey Harold)和李特尔伍德(John Edensor Littlewood)为代表的学派。剑桥大学自牛顿时代开始一直是英国的数学中心,而数学在其教学体制中又占有重要地位。1837年,剑桥数学杂志创刊,供年轻数学家发表研究成果。

剑桥分析学派将严密化的分析及积分方程、测度等工具用于数论、函数论研究,发展起圆法等重要的分析方法,并解决了一大批数学问题。这种将纯粹数学与应用数学互相补充、共同发展的风格扩大到分析学的研究领域,促进了数学各分支的协调发展。
9
波兰学派
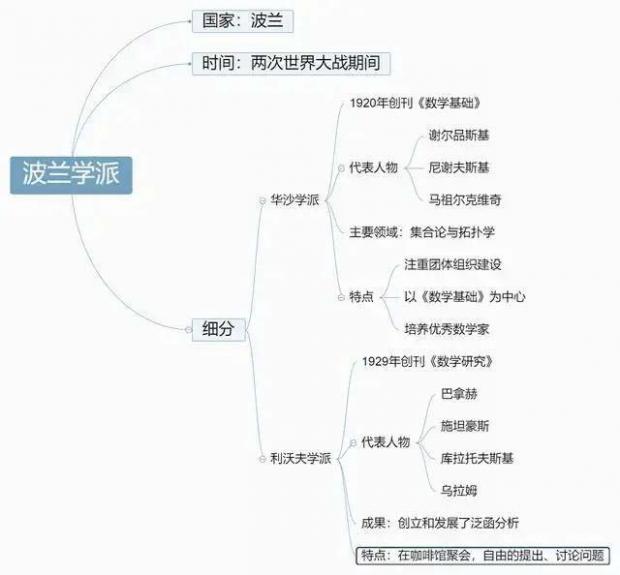
波兰学派兴起于两次世界大战间,依据地点一般又细分为华沙学派和利沃夫学派。华沙学派以1920年创刊的《数学基础》杂志为形成标志;利沃夫学派则以1929年创刊的《数学研究》杂志为代表。两学派的成员分别在两份杂志上发表文章,两份杂志也因此成为了国际上重要的数学杂志。谢尔品斯基(Sierpimski Wactaw)、尼谢夫斯基(Janiszewski Zygmunt)、马祖尔克维奇(Mazurkiewicz)是波兰学派的创始人。他们都曾在华沙大学工作,一起创办了《数学基础》,贡献领域主要在集合论和拓扑学。同时非常注意科学团体的组织建设,以学派刊物为中心,吸引和培养了一大批优秀的数学家。利沃夫学派的代表人物是巴拿赫(Stefan Banach)、施坦豪斯(Steinhaus Hugo Dyonizy)、库拉托夫斯基(Kuratowski Kazimierz)、乌拉姆等人,他们先后学习或执教于利沃夫技术大学,主要是对泛函分析学科的创立和发展做出了贡献。学派常在一个“苏格兰咖啡馆”中聚会,提出和讨论数学问题,其中不乏影响到20世纪后半叶数学发展的问题。除此之外,波兰学派的成员还遍及克拉克夫和波兹南,也促进了波兰数学会及其他科学机构的组建。由于第二次世界大战纳粹的占领,波兰学派随之衰退,幸好战后得到数度复兴。
布尔巴基学派
20世纪30年代出现于法国,由一群青年数学家组成,借用尼古拉·布尔巴基(Nicolas Bourbaki)为集体的笔名,发表数学论文和有关数学基础问题的专著。这群青年在广泛深入地研究现代数学本质的基础上,提出用数学结构的观点对各数学分支进行统一处理,并为此撰写了鸿篇巨著《数学原理》。该书自1939年开始出版以来,已先后出版了近40卷,并陆续被译成英、日、俄等多国文字。同时,还发表500多篇综述当代数学各个领域重大成果的文章。
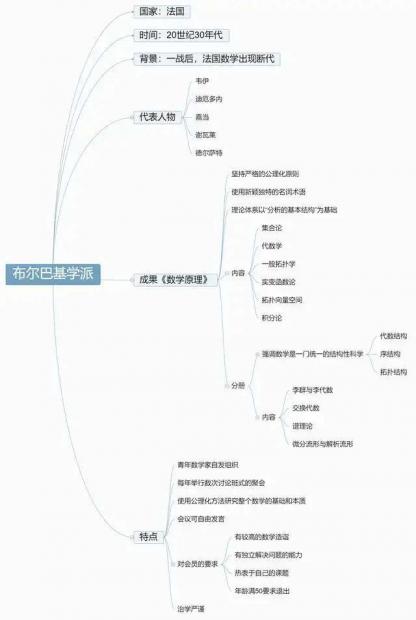
《数学原理》博大精深常,书中坚持严格的公理化原则,并使用新颖独特的名词术语,其理论体系以“分析的基本结构”为基础,内容包括集合论、代数学、一般拓扑学、实变函数论、拓扑向量空间、积分论。此外,还有李群与李代数、交换代数、谱理论、微分流形与解析流形等分册,书中强调数学是一门统一的结构性科学,具有三种基本结构:代数结构、序结构和拓扑结构。数学中的不同分支都是其组成部分。该观点对于丰富人们对数学的认识,推动数学的发展有重要意义,同时也影响了世界各国的数学教育。
20世纪初,直觉主义学派、逻辑主义学派和形式主义学派这3个学派,都是为解决数学基础争论而建立起来的。
 社科在线
社科在线




